Think in IT & Finance: Nelson-Siegel Model Annotated

Link to original Nelson Siegel Model:

https://www.dropbox.com/s/0yj06v5vf4envsy/NelsonSiegel.pdf

1.A Parsimonious Model

Compared with other models like Carleton and Cooper(1976), McCulloch(1971), Echols and Elliott(1976) etc, NS model requires least (only 4) paramters to construct spot yield curve and forward yeild curve.

(1.)Nelson-Siegel Model for spot rate:

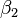$y\left( m \right) = \beta _0 + \beta _1\frac{{\left[ {1 - \exp \left( { - m/\tau} \right)} \right]}}{m/\tau} + \beta _2 {\left(\frac{{\left[ {1 - \exp \left( { - m/\tau} \right)} \right]}}{m/\tau} - \exp \left( { - m/\tau}\right)\right)}$

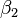where $y\left( m \right)$ and $m$ are as above, and $\beta _0$ , $\beta _1$ , $\beta _2$ and $\tau$ , are parameters to be fitted via a least-square or similar algorithm (see Diebold and Li [2006]):

$\beta _0$ is interpreted as the long run levels of interest rates (the loading is 1, it is a constant that does not decay);
$\beta _1$ is the short-term component (it starts at 1, and decays monotonically and quickly to 0);
$\beta _2$ is the medium-term component (it starts at 0, increases, then decays to zero);
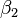$\tau$ is the decay factor: small values produce slow decay and can better fit the curve at long maturities, while large values produce fast decay and can better fit the curve at short maturities; $\tau$ also governs where $\beta _2$ achieves its maximum.

(2.) Nelson-Siegel Model for forward rate:

y(m) = B0+B2*exp(-m/lambda)+B3*(m/lambda)*exp(-m/lambda)

2.Derivation of Nelson-Siegel Model

Assume that forward rates follow a second order diﬀerential equation with two equal real roots:

f''+a*f'+bf=0

Solving this equation gives us the Nelson-Siegel function for forward rates:

y(m) = B0+B2*exp(-m/lambda)+B3*(m/lambda)*exp(-m/lambda)

3.Arbitrage Free and NS Model

The original Nelson Siegel paper describes a parsimonious model of the term structure using only four or three (if

lambda is fixed). Filipovic (1999) proves that this model can never be used in a arbitrage free context, paraphrasing the abstract:

We introduce the class of consistent state space processes, which have the property to provide an arbitrage-free interest rate model when representing the parameters of the Nelson–Siegel (NS) family. (We show that) there exists no nontrivial interest rate model driven by a consistent state space Itō process.

This problem is solved by Christensen et al. (2009). They provide some ODE's which must hold for an AFNS and write that the "key difference between Dynamic NS and AFNS is the maturity dependent yield-adjustment term" and show how to solve for this term.
They show that the yield adjustment term is empirically small and that their model

fares well in out-of-sample prediction, consistently outperforming, for example, the canonical A0(3) model (of Duffee 2002).

4. Pros
1. Simple & Parsimonious - only 3(if lambda is fixed) or 4 parameters
2. Flexible enough to represent the range of shapes generally associated with yield curves: monotonic, humped, and S shaped.

5. Cons
1.Not arbitrage free
2.While relatively successful in forecasting the yield curve, the Nelson-Siegel model tends to have poor fit to highly nonlinear yield curves and at the long end of the term structure, although this can be improved by considering the Svensson (1994) model
3.Nelson-Siegel and Svensson models have poor forecasting performance around the points of non-parallel shifts, hence making them potentially problematic in interest rate risk management(Duration Hedge)

Think in IT & Finance

Friday, November 23, 2012

Nelson-Siegel Model Annotated

No comments: